椭圆方程式

椭圆方程式

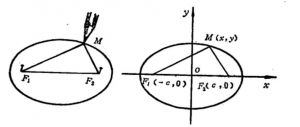
设椭圆的两个焦点分别为F1，F2，它们之间的距离为2c，椭圆上任意一点到F1，F2的距离和为2a（2a>2c）。

以F1，F2所在直线为x轴，线段F1F2的垂直平分线为y轴，建立直角坐标系xOy，则F1,F2的坐标分别为（-c,0)，（c,0)。

设M(x,y)为椭圆上任意一点，根据椭圆定义知

|MF1|+|MF2|=2a，（a>0）

其方程是二元二次方程，可以利用二元二次方程的性质进行计算，分析其特性。

X，Y的范围

当焦点在X轴时 -a≤x≤a,-b≤y≤b

当焦点在Y轴时 -b≤x≤b,-a≤y≤a

对称性

不论焦点在X轴还是Y轴，椭圆始终关于X/Y/原点对称。

顶点：

焦点在X轴时：长轴顶点：（-a，0），（a，0）

短轴顶点：（0，b），（0，-b）

焦点在Y轴时：长轴顶点：（0,-a），（0,a）

短轴顶点：（b,0），（-b,0）

注意长短轴分别代表哪一条轴，在此容易引起混乱，还需数形结合逐步理解透彻 。

焦点：

当焦点在X轴上时焦点坐标F1（-c,0）F2(c,0)

当焦点在Y轴上时焦点坐标F1（0，-c）F2(0,c)

(（其中分别是椭圆的长半轴、短半轴的长，可由圆的面积可推导出来)或（其中分别是椭圆的长轴，短轴的长） 。

圆和椭圆之间的关系：

椭圆包括圆，圆是特殊的椭圆。